Utjämnad interpolering av nyckelbild¶
Har du någonsin undrat varför Kdenlives utjämnade interpoleringsläge kan flöda över mellan nyckelbilder? Och hur säger man till Kdenlive att undvika sådana situationer?
Låt oss börja titta bakom kulisserna och introducera utjämningens konstiga värld. Var inte orolig, det finns inte någon matematik att lära sig och förstå. Titta bara på siffrorna. Vi kommer också att visa hur man undviker sådant överflödande i situationer då man inte vill ha det. Och för de riktigt nyfikna som vill veta vad matematiken bakom ”utjämnad” interpolering är, finns det lite ytterligare läsning i avsnittet Anmärkningar längst ner på sidan.
Intoningsrampen¶
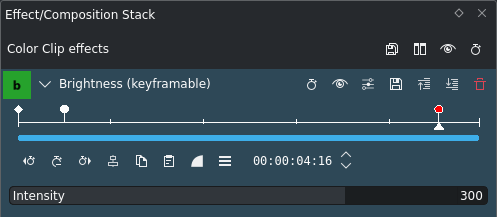
Nyckelbilder för effekten Intensitet¶
Låt oss börja med en enkel ramp, som visas här. Vi använder två nyckelbilder[1], en med en låg värdeinställning och den andra med en hög värdeinställning. De specifika värdena spelar ingen roll. Vi ställer in båda nyckelbilder till interpoleringsläget jämn.

Visning av färgklippets nyckelbild¶
Effektvisningen inuti tidslinjeklippet ser ut som en rak ramp. Men om man tittar noga på de interpolerade värdena medan man följer tidslinjen, bör man märka att rampens lutning varierar. I slutet och början är lutningen mindre än i mitten, där den är större.
Men vad händer egentligen här?
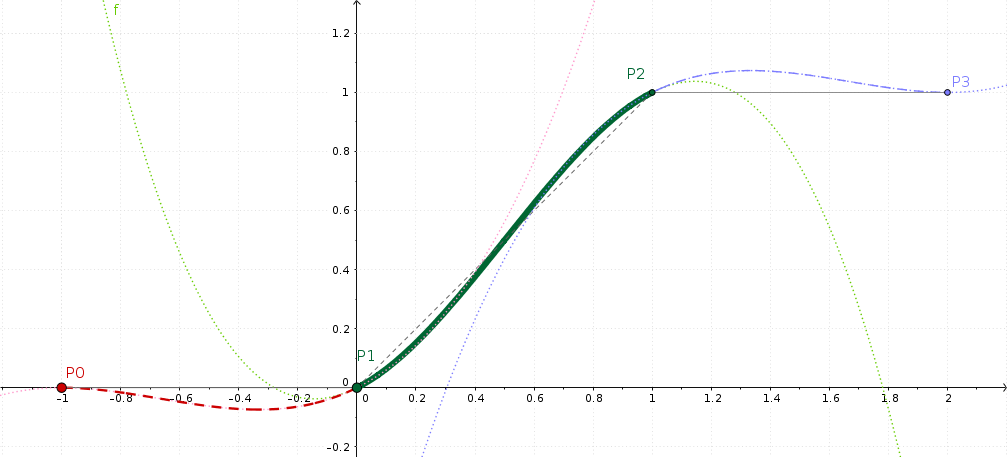
GeoGebra visualisering av Catmull-Rom interpolering¶
Det finns ett verktyg på nätet med öppen källkod, GeoGebra, för att prova matematiken inuti Kdenlives MLT-gränssnitt.
Den här bilden visar två nyckelbilder P1=0 och P2=1, vilket är en ganska typisk inställning av upprampning. Om du redan undrar: det spelar ingen roll vid vilka exakta bildrutor de enskilda nyckelbilderna är.
Den utjämnade interpolationen som MLT beräknar ritas som en bred grön linje. Den är böjd lite som den stora bokstaven S, men trots det egentligen inte för mycket.
Och om man tittar närmare, så är den gröna linjens lutning i början och slutet inte horisontell, trots allt vad som kunde förväntas till en början.
Man kan undra vad de två andra nyckelbilderna P0 och P3 är bra för? Tja, matematiken nedan kräver alltid fyra nyckelbilder för att kunna interpolera segmentvis mellan två intilliggande nyckelbilder. Och om det inte finns någon föregående (P0) eller efterföljande (P1) nyckelbild, upprepar vi helt enkelt vänster (P1) eller höger (P2) nyckelbild.
Rampa upp, och … flöda över¶
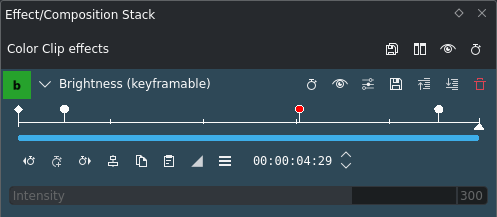
Nyckelbilder för effekten Intensitet¶
Låt oss nu lägga till en tredje nyckelbild, så det ser ut som en ramp med en platå. Det visas på skärmbilderna.
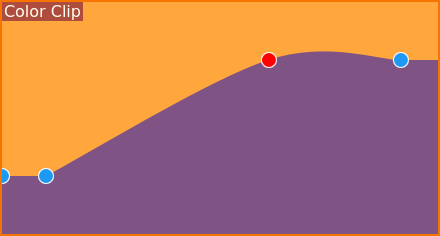
Visning av färgklippets nyckelbild¶
Och nu får rampen en väl synlig bula istället för en skarp krök. Ja, det här ser utjämnat ut, men inte riktigt vad vi kanske hade tänkt oss? Så varför är det som det är?
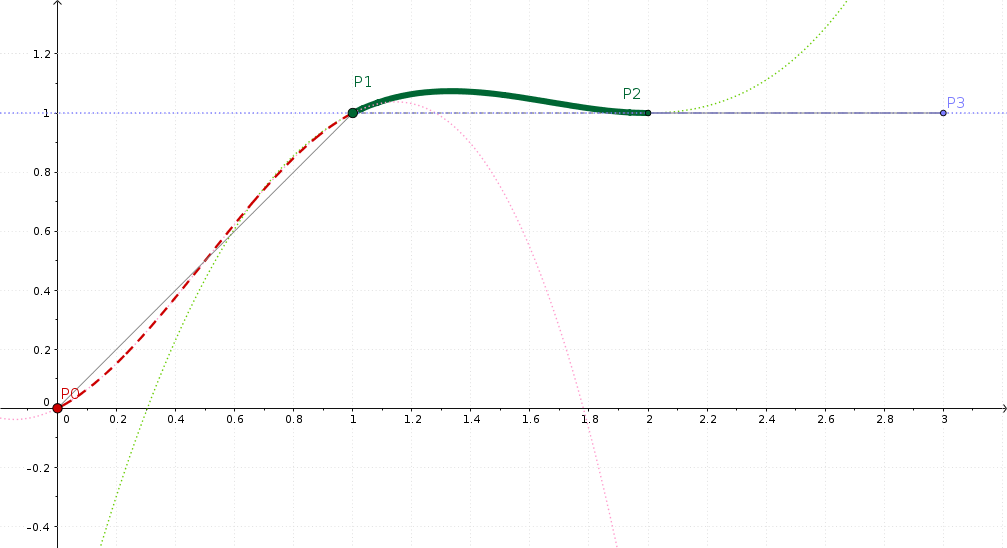
GeoGebra visualisering av Catmull-Rom interpolering¶
Det här är nu vår ramp med en platå: P0=0, P1=1, P2=2. Var dock inte orolig för numreringen av nyckelbilder.
Var förväntningen att platån skulle vara, ja, en rak platå? Självklart var den det. Men det märks redan att Kdenlive inte exakt beter sig så. Istället gör interpoleringsmatematiken att de interpolerade värdena överflödar, vilket enkelt går att se i figuren.
Vad den underliggande matematiken gör är följande: interpoleringen är jämn, så att lutningen till vänster om P1 är densamma som till höger om P1. Ja, det är en lite annorlunda ”utjämnat” än vad man kanske hade förväntat sig.
Om man istället vill att platån ska vara rak, måste man ställa in interpoleringsläget för nyckelbilden P1 till linjär istället. Det ändrar förresten inte det föregående utjämnade segmentet på något sätt. Och det resulterar i en ”grov böjning” vid P1, men som tur är märks det förmodligen inte i de flesta situationer.
Rampa upp, platta ut¶
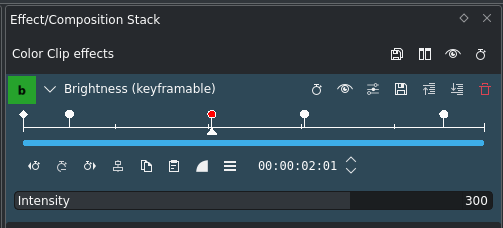
Nyckelbilder för effekten Intensitet¶

Visning av färgklippets nyckelbild¶
Låt oss lägga till en annan, fjärde, nyckelbild, så att vi får: rampa upp först, sedan platt, sedan rampa ner. En ganska typisk nyckelbildsmall för intonings och borttoning.
Och se, vad som händer: vi får en puckel, men inte en snygg och platt mittsektion.
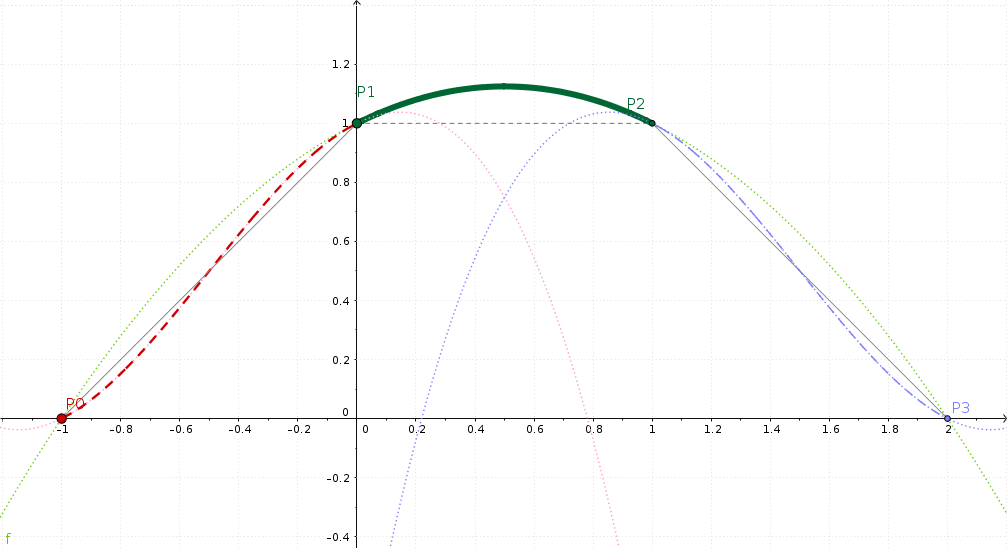
GeoGebra visualisering av Catmull-Rom interpolering¶
Den här gången tittar vi på mittsektionen P1-P2. Till vänster ser vi en upprampning, till höger en nedrampning.
Återigen betyder jämn nu att det inte finns någon skarp böj i segmenten. Istället är vänster och höger lutning kontinuerlig vid P1 och P2, det vill säga i mittsektionen. Och det gör att vårt interpolerade värde flödar över.
Göra rakt bra igen¶
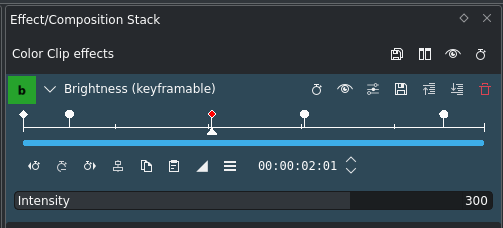
Utjämnade nyckelbilder i effekten Intensitet¶
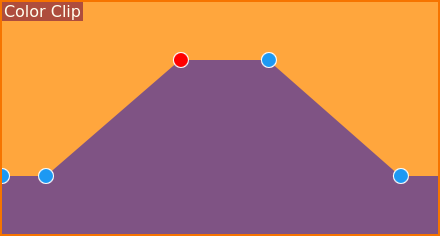
Så, hur får vi en utplattad topp? Lyckligtvis är det lätt att uppnå, som syns på skärmbilderna.
Anmärkningar
- Ytterligare läsning
Som du kanske (eller snarare kanske inte kommer ihåg) är Kdenlives återgivningsgränssnitt MLT Multimedia Framework. Medan MLT har smooth interpolation sedan omkring mitten av 2013 kom Kdenlive ikapp först senare och stöder nu alla tre metoderna att interpolera: linjär, diskret och jämn. Som kan ses från MLT source code, görs utjämnad interpolering med en Catmull-Rom spline. I synnerhet använder MLT den så kallade likformiga varianten, eftersom den är så enkel. Nackdelen är att utjämningen ibland har den oönskade egenskapen att flöda över, i synnerhet när man minst anar det.
- Källor
Den ursprungliga texten skickades in av användaren TheDiveO till den nu nedlagda bloggen kdenlive.org. För den här dokumentation har den hämtats från kdenlive.org, uppdaterats och anpassats för att motsvara den övergripande stilen.