Interpolació de fotograma clau «suau»¶
Alguna vegada us heu preguntat per què el mode d'interpolació suau del Kdenlive pot excedir-se entre fotogrames clau? I com dir-li al Kdenlive que eviti aquestes situacions?
Comencem a mirar les interioritats i us introdueixo en l'estrany món de la suavitat. No us preocupeu, no hi haurà matemàtiques per a aprendre i entendre. Només mireu les xifres. També us mostrarem com evitar aquests excessos en aquelles situacions que no els vulgueu. I per als curiosos de les matemàtiques darrere de la interpolació «suau» hi ha algunes lectures addicionals a la secció Notes de la part inferior d'aquesta pàgina.
La rampa de fosa d'entrada¶
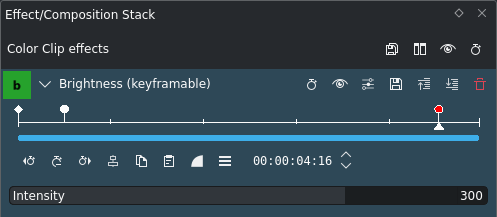
Fotogrames clau en l'efecte Lluminositat (amb fotogrames clau)¶
Comencem amb una rampa simple, com es mostra aquí. Utilitzem dos fotogrames clau[1], un amb un valor baix i l'altre amb un valor alt. Els valors en particular no importen. Hem establert ambdós fotogrames clau al mode d'interpolació suau.
Visualització de fotograma clau del clip de color¶
L'efecte que es mostra dins del clip de la línia de temps sembla una rampa recta. Però si observeu els valors interpolats de prop mentre s'escombra la línia de temps, haureu d'adonar-vos que el pendent de la rampa varia. Al final i al principi el pendent és més petit que al mig, on és més alt.
Però, què ocorre exactament aquí?
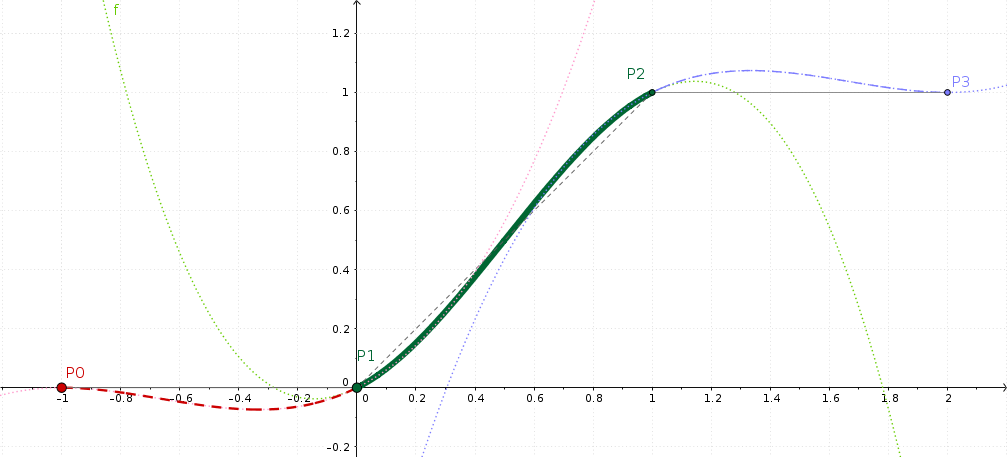
Visualització GeoGebra de la interpolació Catmull-Rom¶
Hi ha aquesta eina de codi obert en línia GeoGebra per a provar les matemàtiques dins del motor MLT del Kdenlive.
Aquesta figura mostra dos fotogrames clau P1=0 i P2=1, que és una configuració de rampa bastant típica. Per si ja us pregunteu: no importa en quins marcs exactes es troben els fotogrames clau individuals.
La interpolació suau que calcularà el MLT es dibuixa com una línia verda gruixuda. S'inclina una mica com la lletra majúscula S, però tampoc gaire.
I si mireu de prop, el pendent inicial i final de la línia verda no són horitzontals, almenys el que es podria esperar d'entrada.
Pot ser que us pregunteu per a què serveixen els altres dos fotogrames clau P0 i P3? Bé, les matemàtiques subjacents sempre requereixen quatre fotogrames clau per tal d'interpolar respecte al segment entre dos fotogrames clau adjacents. I si no hi ha un fotograma clau anterior (P0) o posterior (P1), llavors repetirem el fotograma clau esquerre (P1) o dret (P2).
Rampa amunt i… excés¶
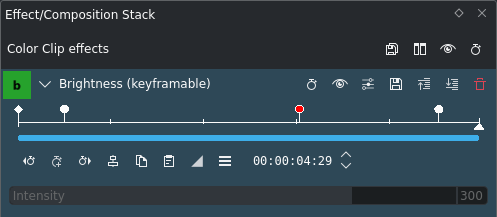
Fotogrames clau en l'efecte Lluminositat (amb fotogrames clau)¶
Ara afegirem un tercer fotograma clau, així que sembla una rampa amb un altiplà. Això es mostra en les captures de pantalla.
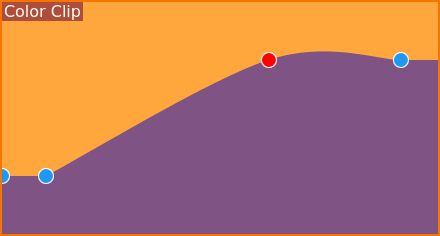
Visualització de fotograma clau del clip de color¶
I ara, la rampa té un bony clarament visible en lloc d'una corba fina. Bé, això sembla suau, però no és exactament el que podríem haver pensat? Per què és així?
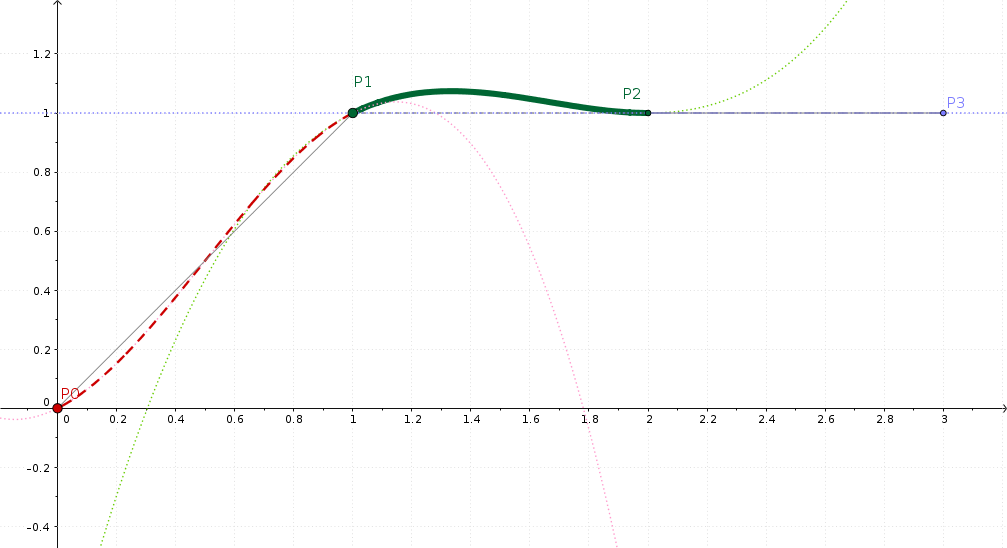
Visualització GeoGebra de la interpolació Catmull-Rom¶
Aquesta és ara la nostra rampa amb un altiplà: P0=0, P1=1, P2=2. Però no us preocupeu per la numeració dels fotogrames clau.
Esperàveu que l'altiplà fos un altiplà recte? Clar. Però ja us heu adonat que el Kdenlive no es comporta exactament així. En lloc d'això, les matemàtiques d'interpolació provoquen que els valors interpolats s'excedeixin, com es pot veure fàcilment en la figura.
El que fan les matemàtiques subjacents és això: la interpolació és suau, de manera que el pendent de la esquerra de P1 és el mateix que la dreta de P1. Sí, això és un «suau» lleugerament diferent del que es podia esperar.
Si voleu que l'altiplà sigui recte, llavors heu d'establir el mode d'interpolació del fotograma clau P1 a lineal. Per cert, això no canvia el segment suau previ de cap manera. I això dona lloc a una «corba difícil» a P1, però per sort probablement no us adonareu en la majoria de situacions.
Rampa amunt-pla-avall¶
Fotogrames clau en l'efecte Lluminositat (amb fotogrames clau)¶
Visualització de fotograma clau del clip de color¶
Afegim un quart fotograma clau, així que tenim: rampa amunt primer, després pla, després rampa avall. Un patró de fotograma clau de fosa d'entrada i fosa de sortida força típica.
I mireu què passa: tenim un bon gep, però no una secció central acurada i plana.
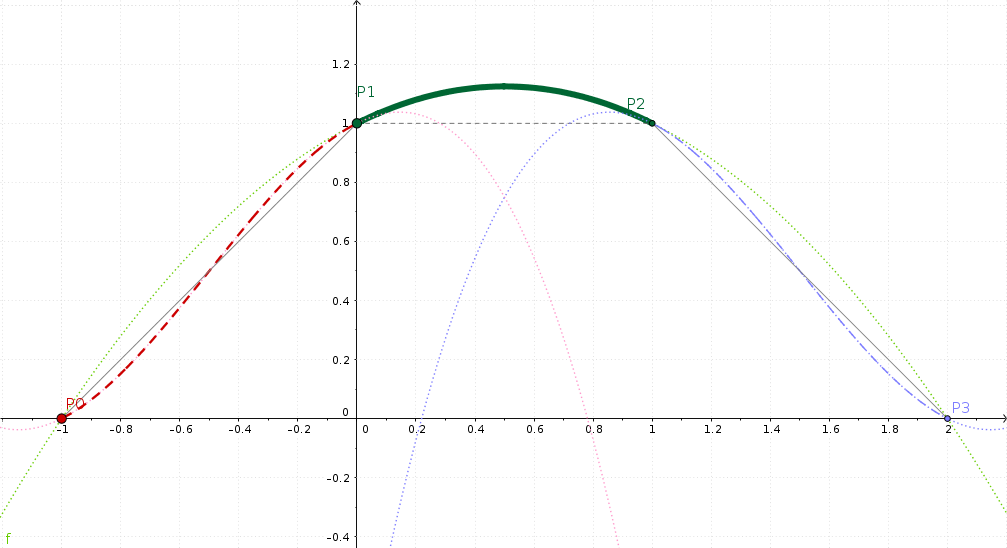
Visualització GeoGebra de la interpolació Catmull-Rom¶
Aquesta vegada, observem la secció central P1-P2. A l'esquerra, veiem la rampa amunt, a la dreta, la rampa avall.
De nou, suau ara significa que no hi ha cap corba afilada en els segments. En canvi, els pendents de l'esquerra+dreta són continus a P1 i P2; és a dir, a la secció central. I això fa que el nostre valor interpolat sigui excessiu.
Tornem a fer gran el pla¶
Fotogrames clau suaus en l'efecte Lluminositat (amb fotogrames clau)¶
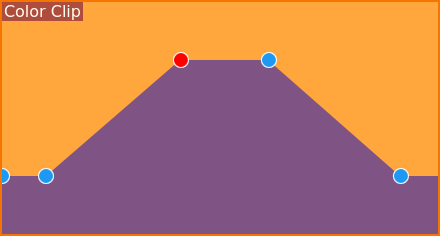
Ara, com podem aconseguir un capdamunt pla? Afortunadament, és fàcil d'aconseguir, com es pot veure en les captures de pantalla.
Notes
- Lectura addicional
Com podeu (o potser no) recordar, el motor de representació del Kdenlive és el MLT Multimedia Framework. Mentre que el MLT té smooth interpolation des de mitjans de 2013, el Kdenlive només es va posar al dia més tard i ara admet tots tres modes d'interpolació: lineal, discret i suau. Com es pot veure des del source code del MLT, la interpolació suau es fa utilitzant una Catmull-Rom spline. En particular, el MLT utilitza l'anomenada variant uniforme, perquè és tan simple. El desavantatge és que aquest suavitzat a vegades té la propietat no desitjada d'excedir-se, especialment quan menys s'espera.
- Fonts
El text original va ser enviat per l'usuari TheDiveO al blog kdenlive.org, ja desaparegut. Per a aquesta documentació s'ha extret de kdenlive.org, s'ha actualitzat i adaptat per a concordar amb l'estil general.