Sestavljanje s prosojnostjo

Kadar je prosojnost prisotna v obeh sličicah, ki ju obdeluje eden od prehodov za dinamično sestavljanje v Kdenlive, je rezultat za nekatere uporabnike morda presenetljiv. Na srečo stvari niso tako nerazložljive, kot se zdijo, zato se takoj potopimo v prosojnost in prehode.

Prosojnost in dinamični prehodi

Ko gre za ravnanje s prosojnostjo, se v Kdenlive prehodi delijo na dve kategoriji:

1. Afino: uporablja t.i. operator skladanja zgoraj.

2. Sestavljeno, Sestavljeno in preoblikuj, (Afino) spajanje Kairo: namesto tega uporablja operator sestave preko.

Kaj torej pomenita ta zgoraj in preko v resnici? Odkrijmo, kaj ti operaterji sestave storijo s tipičnim primerom napisa in polprosojnega ozadja. Za preprostost bomo najprej ignorirali parameter prekrivnosti prej omenjenih prehodov, da bo stvari lažje dojeti. In potem, ko bomo obvladali ta korak, bomo končno pogledali, kako se parameter prekrivnosti ujema s celotno sliko.

Afino: skladanje na vrhu

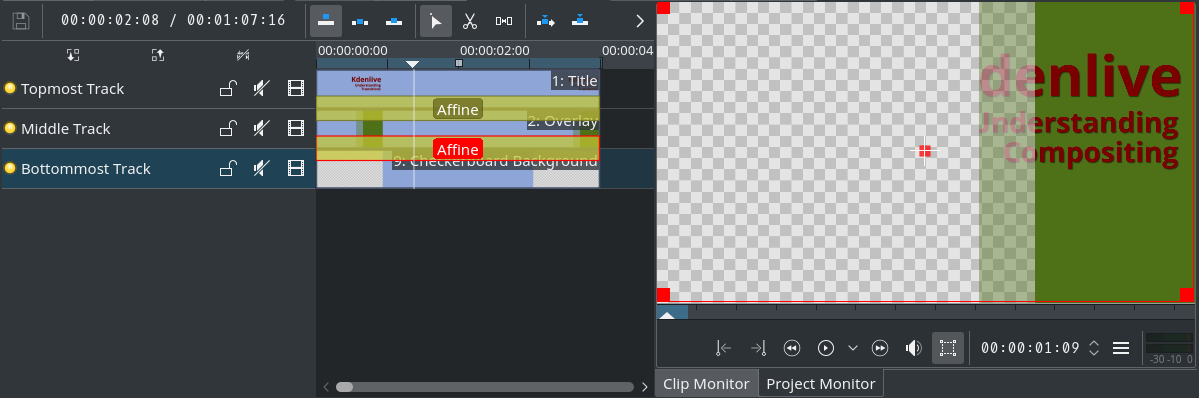
Rezultat sestave zgoraj je najbolje razložiti na začetku s prikazom njenega izida: besedilo iz najvišjega posnetka napisa (delno) izgine v tistih področjih, kjer je podležni posnetek na srednji stezi (pol)prosojen.

Posnetek s šahovnico na spodnji stezi služi le za namene ilustracije, da lahko bolje vidimo prosojna območja.

Prosimo, upoštevajte, kako sta dva afina prehoda verižena: najprej zgornji afini sestavi posnetek napisa na ozadje preliva. Nato spodnji afini sestavi rezultat na ozadje šahovnice.

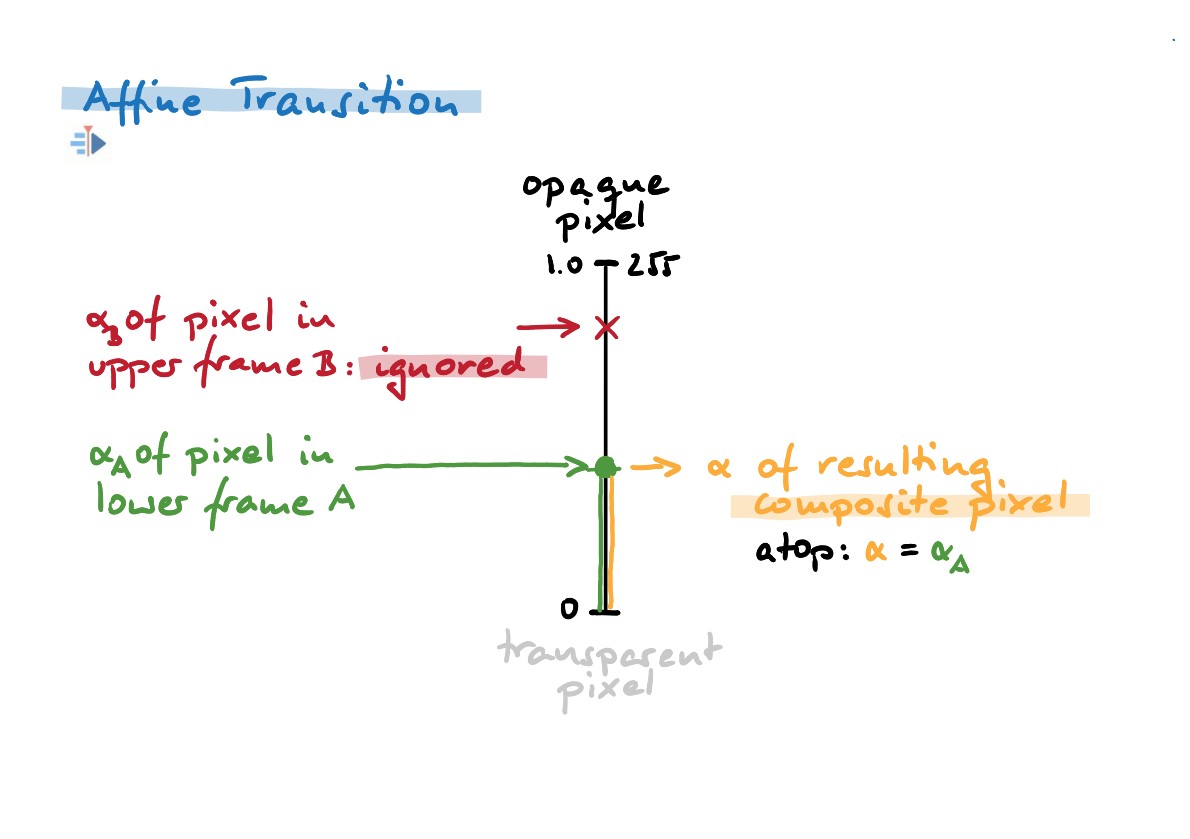
Toda kako afini prehod natančno obravnava prosojnost? Poglejmo si to ročno izdelano ilustracijo, kjer imamo dve slikovni točki, vsako z nekaj prosojnosti (alfa-vrednosti, αA in αB). Pomembno je, da ne zamešamo prosojnosti slikovnih točk s parametrom prekrivnosti prehodov.

Naša rdeča slikovna točka izvira iz sličice zgornje steze (B), zelena slikovna točka pa iz sličice spodnje steze (A). Alfa 0 pomeni popolnoma prosojno slikovno točko, alfa 1,0 (ali 255) pa popolnoma prekrivno slikovno točko.

Afini prehod zdaj preprosto prezre informacije o prosojnosti iz slikovne točke zgornje sličice (rdeče).

Uporablja samo informacije o prosojnosti (zeleno), vsebovano v sličicah spodnjih stez! Ali bolj matematično: α = αA

In to je razlaga, zakaj v našem primeru nad besedilo napisa izgine na tistih območjih, kjer je srednji posnetek prosojen.

Sestavljeno in sorodniki: o sestavljanju

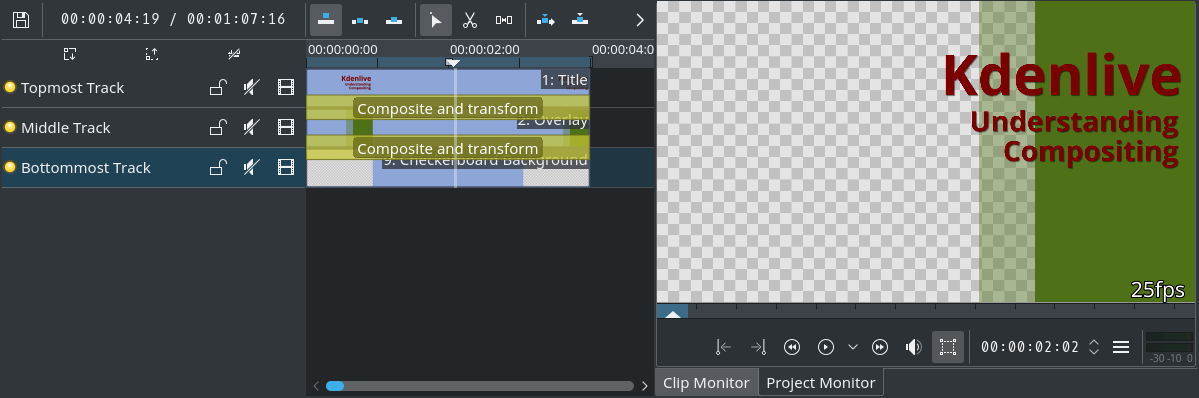
Spet v bistvu uporabljamo enako nastavitev kot prej, tokrat pa uporabimo Sestavljeno in preoblikuj namesto affinih prehodov. Prehode verižimo kot prej, tako da bo nižji prehod deloval na izidu zgornjega prehoda.

Ampak poglejte! Izid je drugačen! Rezultat operatorja prek je verjetno bolj pričakovan za večino uporabnikov. Zgornji posnetek naslova (žal) ni več porezan.

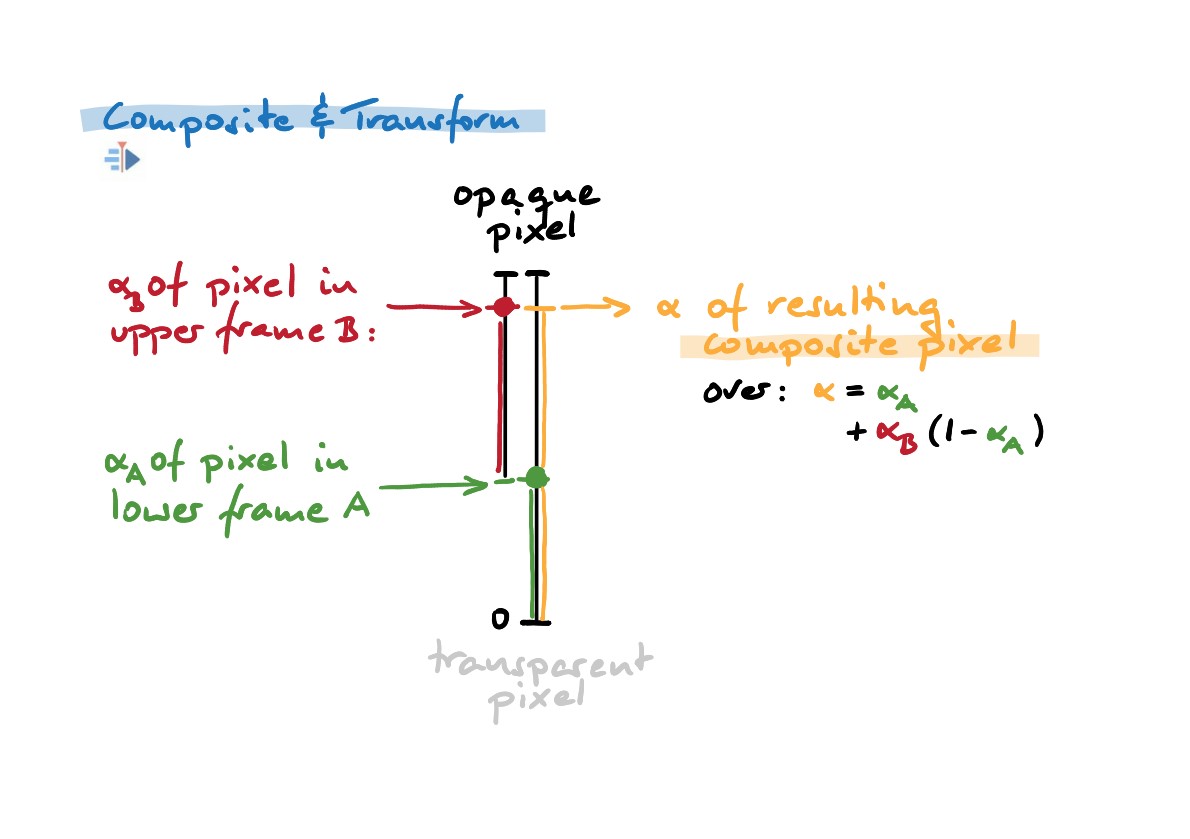
Ker operacija preko bolj izkaže pričakovanja številnih uporabnikov, kako natančno ravna s prosojnostjo?

Preprosto povedano: če pobarvaš neko polprosojno slikovno točko preko druge polprosojne slikovne točke, potem bo rezultat manj prosojen. Še manj prosojno bo od slikovne točke prosojnosti spodnje sličice. To bi verjetno pričakovali od slikanja s polprekrivno barvo.

Tako je tokrat izračun posledične prosojnosti za dani slikovni točki iz zgornje sličice (B) in spodnje sličice (A) bolj zapleten.

Spet začnemo s prosojnostjo (zelene) slikovne točke spodnje sličice kot osnovo. Tokrat pa ne moremo prezreti prosojnosti (rdeče) slikovne točke zgornje sličice. Toda preprosto seštevanje obeh prosojnosti ne bi prineslo smiselnih rezultatov; kaj pomeni prosojnost 2,0 ali 511?

Zato je prosojnost rdeče slikovne točke skalirana: morda pomislite, da bi se prvotna lestvica 0-1,0 skrčila v razpoložljiv prostor nad vrednostjo prosojnosti zelene. Rezultat prosojnosti je potem vsota osnovne alfa-vrednosti zelene plus preskalirana alfa-vrednost rdeče. Pomnite, nekako prebarvamo spodnjo sličico. Za formularno-afino: α = αA + αB (1-αA)

Parameter prekrivnosti prehoda

Prehodi dinamične sestave imajo tudi parameter, imenovan Prekrivnost. Enostavno ga je zamešati s prosojnostjo slikovne točke, vendar pomeni nekaj drugega. Parameter prekrivnost velja samo za zgornje sličice (B). To je kot nekakšen glavni nadzor, vendar kako deluje?

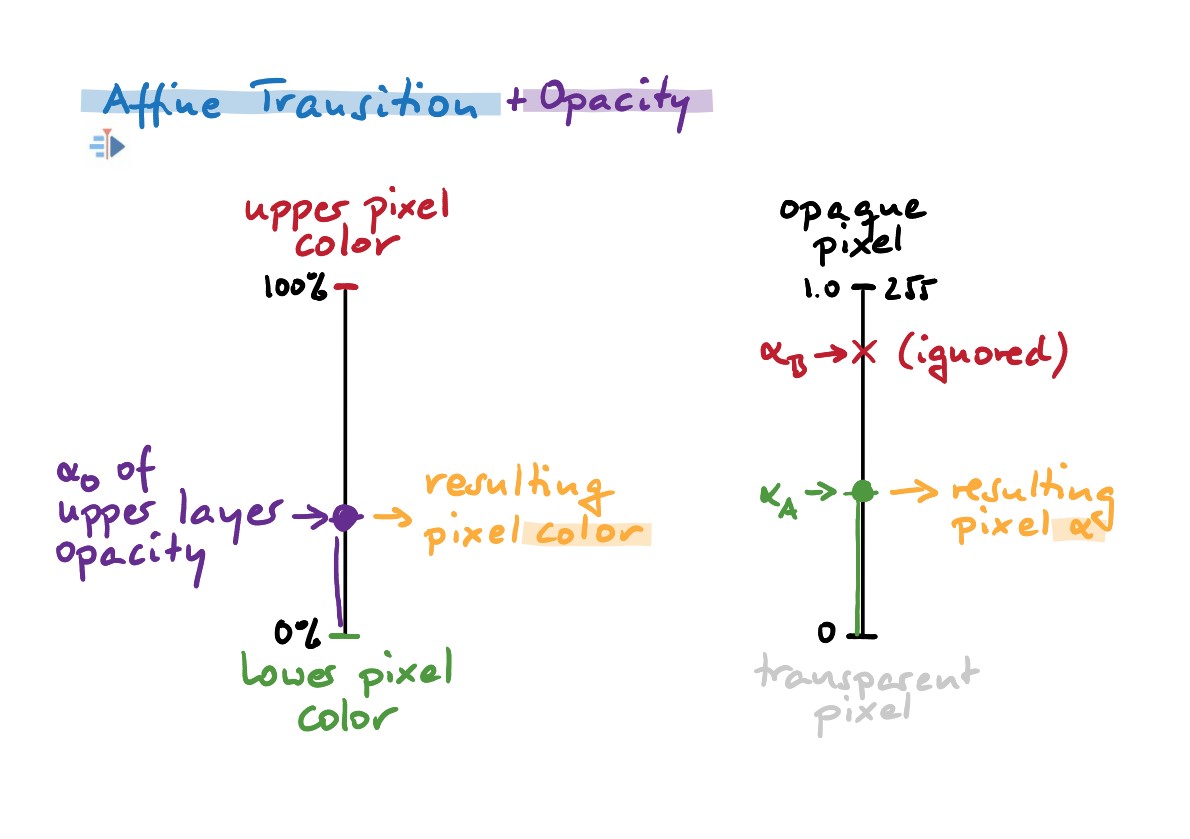
Začnimo z afinim prehodom, znova. Zgoraj smo videli, da afino prezre prosojnost (rdečih) slikovnih točk zgornje sličice. In afino prezre tudi parameter prekrivnosti pri izračunu rezultatov prosojnosti slikovnih točk.

Namesto tega parameter prekrivnosti vpliva na to, kako se izračuna barva slikovne točke rezultata: to je linearna interpolacija med barvo slikovne točke zgornje sličice (B) in slikovne točke spodnje sličice (A). Prekrivnost zdaj nadzoruje natanko točko mešanja. Prekrivnost 0,0 ima za rezultat le barvo slikovne točke spodnje sličice (B), 1,0 pa daje samo barvo slikovne točke zgornje sličice (A). 0,5 bi bil na polovici med barvama obeh slikovnih točk.

Če povzamem:o v primeru afinega prehoda parameter prekrivnost vpliva samo na barvno mešanje med slikovnimi točkami zgornje sličice (B) in spodnje sličice (A).

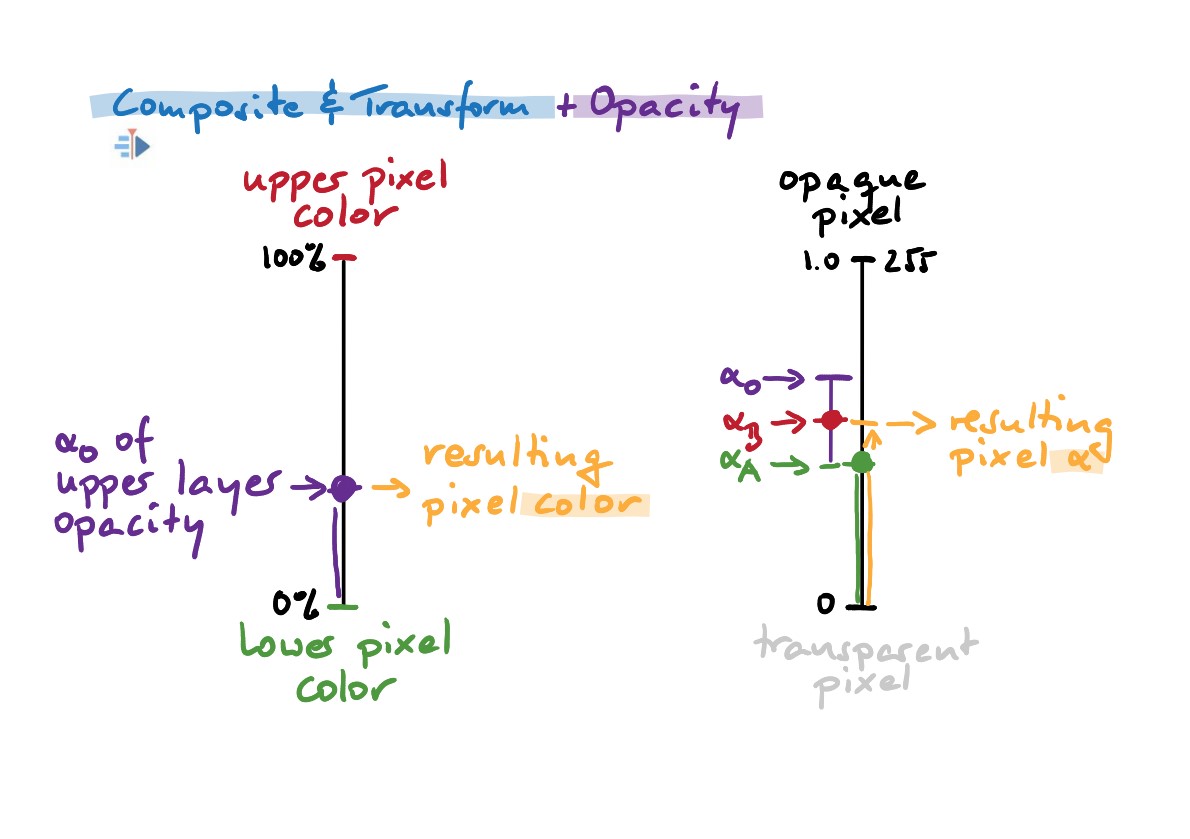
Nato si poglejmo še druge prehode: Sestavljeno in prijatelji.

Kar zadeva barvno mešanje, velja enak postopek, kot smo ga pravkar videli z afinim prehodom: parameter prekrivnosti nadzoruje, koliko barve slikovne točke zgornje sličice (B) pride v mešanico.

Ko pa pogledamo, kako se izračuna prosojnost slikovne točke rezultata, stvari začnejo izgledati drugačne. Videli smo, da se prosojnost slikovne točke zgornje sličice (B) zmanjša v obratnem deležu prosojnosti slikovne točke spodnje sličice (A). Parameter prekrivnosti to še dodatno podkrepi: dodatno zmanjša prosojnost slikovne točke zgornje sličice (B). Oglejte si tudi ilustracijo.

Posledično parameter prekrivnosti tako nadzoruje, koliko prekrivnosti slikovne točke zgornje sličice (B) se sploh uveljavi. Na ta način lahko odtemnite ali zatemnite zgornjo sličico.

Če povzamemo: v primeru prehodov Sestavljeno (in sorodnih), parameter prekrivnosti vpliva tako na barvno mešanje slikovnih točk zgornje sličice (B) in spodnje sličice (A), kot tudi na prosojnost zgornje sličice (B).

Opombe

Nadaljnje branje

• Članek v Wikipediji o sestavljanju alfe Alpha Compositing s sklicevanjem na izvirni članek Porterja Duffa s konference SIGGRAPH’84 »Compositing Digital Images«.

• SVG Open 2015 paper Craiga Northwaya na temo »Razumevanje sestavljanja in barvnih razširitev v SVG 1.2 v 30 minutah!« - glejte zlasti tabelo Porter Duffovega operatorja v poglavju 6 s stolpcem za izračun alfa.

Viri

Izvirno besedilo je uporabnik TheDiveO poslal na zdaj že ukinjen blog kdenlive.org. Za to dokumentacijo je bilo povzeto iz kdenlive.org, posodobljeno in prilagojeno, da ustreza splošnemu slogu.