Увага
Супровід даних на цій сторінці припинено — тут містяться дані щодо можливостей або функцій попередніх версій Kdenlive, які вважаються застарілими або які було замінено якимись іншими можливостями програми.
Афінний перехід¶
Виконує обертання зображення у просторі, перекошування та викривлення зображення.
Визначає анімовані афінні перетворення за ключовими кадрами із можливостями розчинення зображення.
У багатьох випадках цим переходом можна скористатися замість композиційного переходу. Його використання надає змогу уникнути проблеми із «позеленінням», про яку повідомляли деякі користувачі. (Mantis 2759)
Приклад 1¶
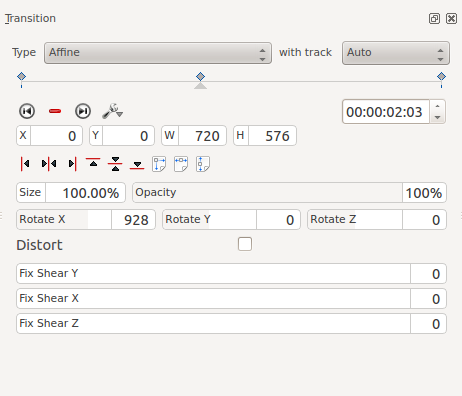
Розчинення за допомогою афінного переходу¶
Щоб додати розчинення, змініть рівень непрозорості до нуля відсотків.
Обертання за допомогою афінного переходу¶
Для обертання зображення додайте ключовий кадр і введіть значення кута обертання. Одиницями запису є десяті частки градуса (тобто 900 означає обертання на 90 градусів).
Обертання навколо X обертає кадр у площині екрана. Параметри Обертання навколо Y та Обертання навколо Z створюють ілюзію обертання у просторі, якщо використовувати їх динамічно із ключовими кадрами — див. наведений нижче приклад.
Подібний ефект можна створити за допомогою ефекту Обертання (за ключовими кадрами) з групи ефектів обрізання та перетворення.
Приклад 2 — обертання за Y¶
Цей приклад створено за допомогою 3 ключових кадрів. Нижче показано другий ключовий кадр із значенням параметра Обертання навколо Y рівним 180O (=180 градусів). Для першого і третього ключових кадрів встановлено нульове значення параметра Обертання навколо Y.
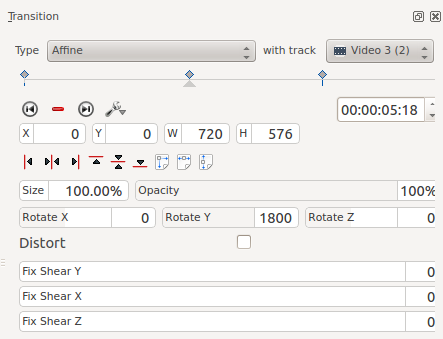
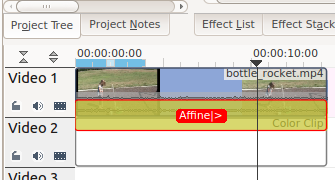
Відмінністю між пунктами Обертання навколо Y та Обертання навколо Z полягає у тому, що видиме обертання для пункту Обертання навколо Y виконується навколо горизонтальної вісі, а обертання для пункту Обертання навколо Z виконується навколо вертикальної вісі.