Vloeiende interpolatie van keyframe¶
Vroeg u zich ooit af waarom Kdenlive’s vloeiende interpolatie mode soms een overshoot heeft tussen keyframes? En hoe u Kdenlive zodanig instelt dat het dergelijke situaties vermijdt?
Laten we beginnen om achter het gordijn te kijken en u te introduceren in de vreemde wereld van vloeiend. Geen zorgen, er zal niets wiskundig voor u zijn om te leren en te begrijpen. Kijk naar de figuren. We zullen ook u ook tonen hoe zulk te ver gaan in die situaties, die u niet wilt, te vermijden. En voor de echt nieuwsgierigen die willen weten wat het wiskundige is achter “vloeiende” interpolatie is er enig meer te lezen in de sectie Notities onderaan deze pagina.
De stijging van fade-in¶
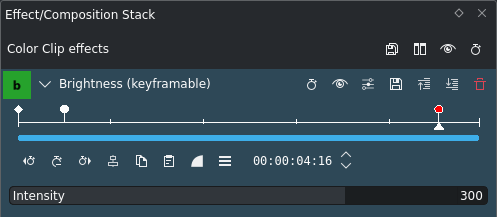
Keyframes in het effect doc:/effects_and_filters/video_effects/color_image_correction/brightness_keyframable¶
Laten we beginnen met een eenvoudige helling, zoals hier getoond. We gebruiken twee keyframes[1], een met een lage waarde instelling en de ander met een hoge waarde instelling. De specifieke waarden zijn niet belangrijk. We zetten beide keyframes in de interpolatiemodus vloeiend.

Weergave van kleurclipkeyframe¶
Het effect dat in de tijdlijn getoond word lijkt op een rechte lijn. Maar als u de geïnterpoleerde waarde nauwkeurig bekijkt tijdens het doorwandelen van de tijdlijn, dan zal u opmerken dat de hellingshoek van de lijn varieert. Aan het eind en aan het begin is de hellingshoek kleiner dan in het midden, waar de hellingshoek groter is.
Maar wat is hier exact gaande?
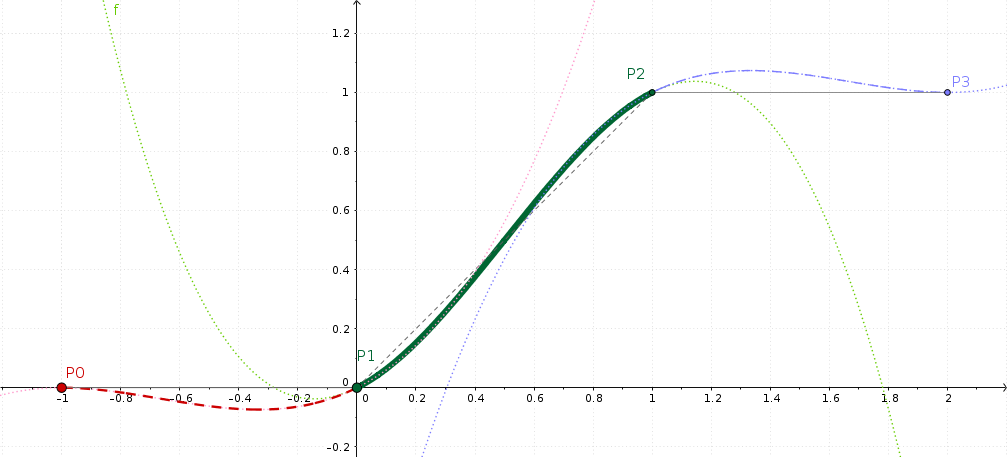
GeoGebra visualisatie van de Catmull-Rom interpolatie¶
Er is dit online open-source hulpmiddel GeoGebra voor het uitproberen van de wiskunde in de MLT-engine van Kdenlive.
Deze figuur toont twee keyframes P1=0 en P2=1, wat een tamelijk gewone opzet is voor een helling. Voor het geval u zich afvraagt: het doet er niet toe op welke exacte frames de individuele keyframes zich bevinden.
De vloeiende interpolatie die MLT zal berekenen wat is getekend als een dikke groene lijn. Het is een beetje gekromd zoals de hoofdletter S, maar, niet echt veel.
En als u goed kijkt, het begin en eind van de helling van de groene lijn zijn niet horizontaal - wat als eerste zouden verwachten.
U zult zich afvragen waar de twee andere keyframes P0 en P3 goed voor zijn? Wel, het wiskundige eronder vereist altijd vier keyframes om per segment te interpoleren tussen twee naast elkaar liggende keyframes. En als er geen voorgaande (P0) of achtergaande (P1) keyframe is, dan zullen we eenvoudig de linker (P1) of rechter (P2) keyframe herhalen.
Stijgen en …overshoot¶
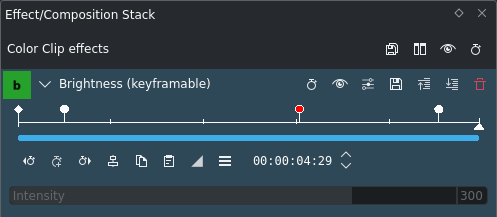
Keyframes in het effect doc:/effects_and_filters/video_effects/color_image_correction/brightness_keyframable¶
Laten we nu een derde keyframe toevoegen, dit lijkt dus als een helling met een plateau. Dit is getoond in de schermafdrukken.
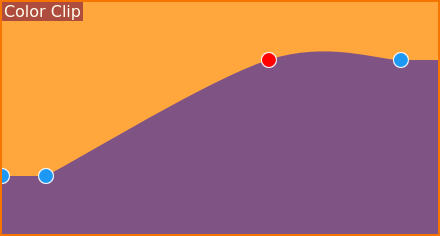
Weergave van kleurclipkeyframe¶
En nu krijgt de helling een duidelijk zichtbare bobbel in plaats van de verwachte scherpe bocht. Wel, dit lijkt vloeiend, maar is niet exact wat we wilde? Waarom is dit op de manier waarop het is?
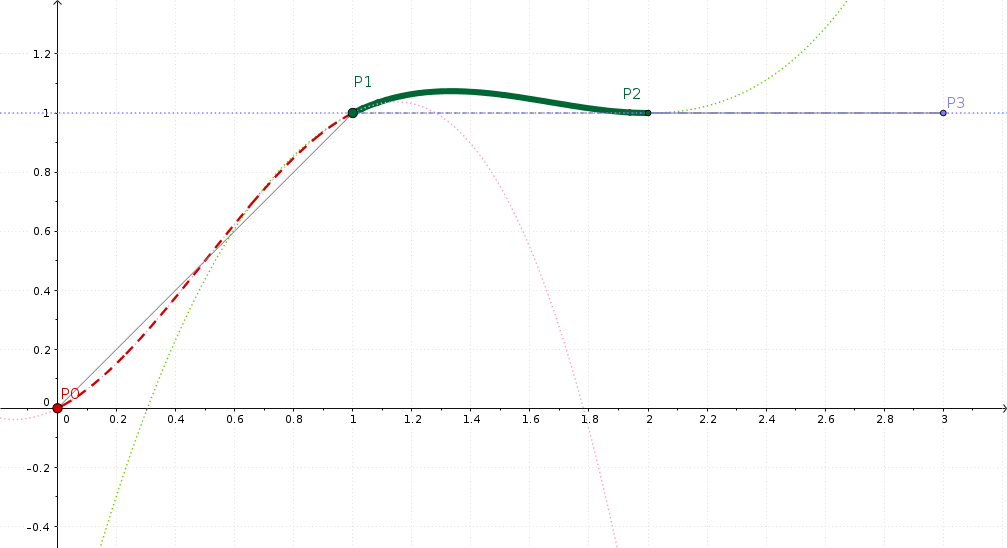
GeoGebra visualisatie van de Catmull-Rom interpolatie¶
Dit is nu onze helling met een plateau: P0=0, P1=1, P2=2. Maakt u zich echter geen zorgen over de nummering van de keyframes.
Verwachte u dat het plateau, wel, een recht plateau zou zijn? Uiteraard verwachte u dat. Maar u zal wellicht al hebben opgemerkt dat Kdenlive zich niet exact zoals dit gedraagt. In plaats daarvan veroorzaakt de wiskunde van de interpolatie dat de interpolatie-waarden een overshoot hebben, zoals u makkelijk in het figuur kan zien.
Wat de onderliggende wiskunde doet is dit: de interpolatie is vloeiend, zodat de helling aan de linkerkant van P1 is hetzelfde als aan de rechterkant van P1. Yeah, dat is een beetje andere “vloeiend” dan u wellicht verwachtte.
Als u in plaats daar van wilt dat het plateau recht is, dan moet u de interpolatie mode van de keyframe P1 instellen op lineair. Op deze manier, verandert dit niet het vorige vloeiende segment op enige manier beïnvloedt. En dit resulteert in een “scherpe bocht” op P1, maar gelukkig zal u dit in de meeste situaties niet merken.
Stijgen-Plat-Dalen¶
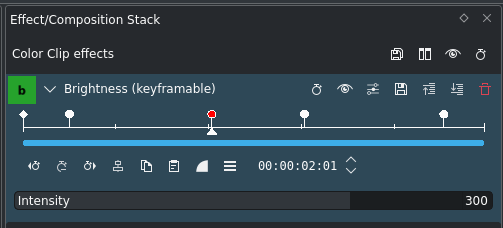
Keyframes in het effect doc:/effects_and_filters/video_effects/color_image_correction/brightness_keyframable¶

Weergave van kleurclipkeyframe¶
Laten we nog een vierde keyframe toevoegen, zodat we dan krijgen: eerst een stijgende helling, dan een plat stuk en tenslotte een dalende helling. Een nogal standaard fade-in en fade-out keyframe sjabloon.
En zie, wat er gebeurt: we hebben een bobbel gekregen, maar geen mooie en eenvlakke midden sectie.
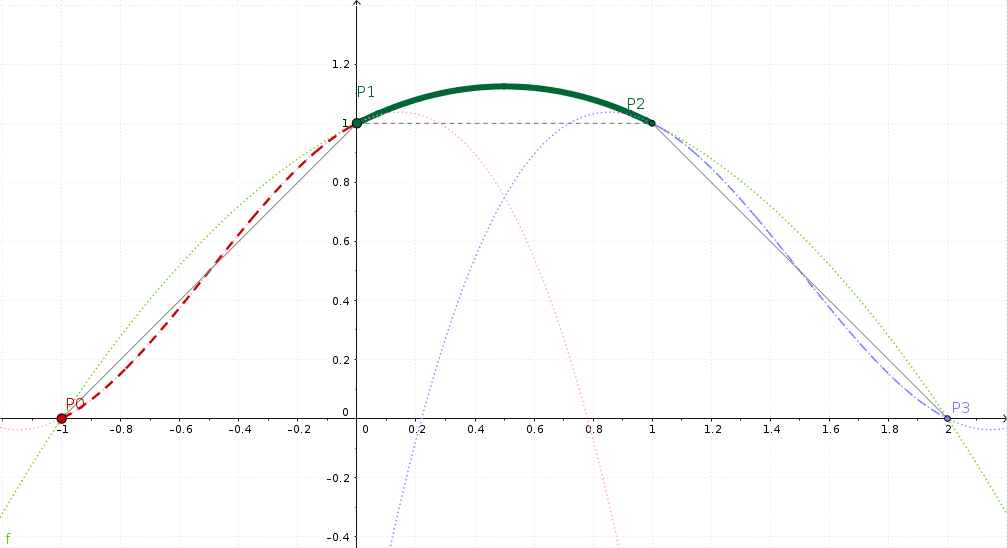
GeoGebra visualisatie van de Catmull-Rom interpolatie¶
Deze keer kijken we naar de middelste sectie P1-P2. Aan de linkerkant zien we de stijging, en aan de rechterkant zien we de daling.
Opnieuw, een vloeiend betekent nu dat er geen scherpe bocht in de segmenten is. In plaats daarvan zijn de linker+ rechter hellingen continu in P1 en P2; dat is in het middelste segment. En dit veroorzaakt dat onze geïnterpoleerdewaarde een overshoot heeft.
Maak plat weer geweldig¶
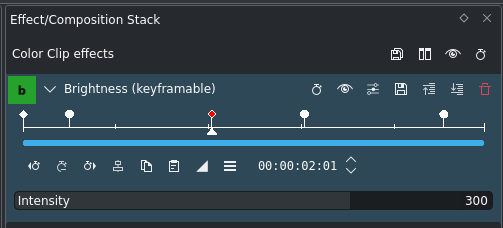
Vloeiende keyframes met het Intensiteit effect¶
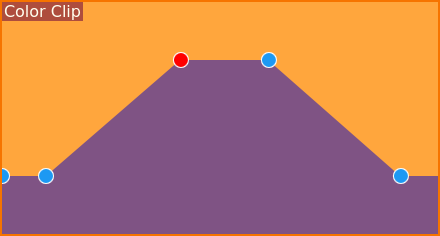
Hoe krijgen we nu een platte top? Gelukkig is dat makkelijk te bereiken, zoals u kan zien in de schermafdrukken.
Notities
- Verdere leesstof
Zoals u zich wellicht (of waarschijnlijk niet) herinnert, Kdenlive’s rendering engine is het MLT Multimedia Framework. Ofschoon MLT smooth interpolation heeft vanaf ongeveer mid-2013, heeft Kdenlive de achterstand ingehaald en kan nu met alle drie interpolatie modes lineair, In stapjes, en vloeiend overweg. Zoals we kunnen zien in de|source_code|, wordt vloeiende interpolatie uitgevoerd met gebruik van een `Catmull-Rom spline. Met name MLT gebruikt de zogeheten uniform variant, omdat deze vrij eenvoudig is. Het nadeel is dat het vloeiend maken soms de ongewenste eigenschap heeft van overshooting, speciaal op die momenten wanneer u het niet verwacht.
- Bronnen
De originele tekst was ingediend door TheDiveO op de nu niet meer functionerende kdenlive.org blog. Voor deze documentatie is het uit het kdenlive.org gehaald, bijgewerkt en aangepast om te voldoen aan de stijl van het geheel.