Interpolación suave de claves¶
¿Alguna vez surgió la duda de por qué sucede que al usar la interpolación Suave en ciertos fotogramas clave de una animación, es posible que la curva de animación sobrepase el valor de los propios fotogramas clave, entre medio de dos de ellos? …y de si existe una forma de decirle a Kdenlive que evite que eso suceda.
Comenzaremos mirando entre bambalinas para hacer una introducción al extraño mundo del suavizado. No hay de qué preocuparse, no expondremos ninguna operación matemática que deba ser comprendida o recordada. Bastará simplemente con observar las figuras. También se mostrará cómo evitar ese tipo de desborde de las curvas en situaciones en donde no se desee tal cosa. Y para el realmente curioso, que desee saber qué operaciones matemáticas hay detrás de la interpolación “suave”, se proporcionará una lectura adicional en la sección de Notas al final de esta página.
La rampa de fundido entrante¶
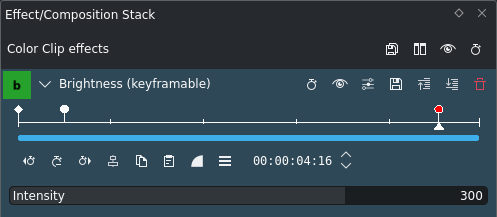
Fotogramas clave en el efecto Intensidad¶
Comencemos con una rampa simple, tal como se muestra aquí. Se insertan dos claves[1], uno con un valor bajo y uno con un valor más alto. Los valores específicos no son de interés. Se utiliza en ambos claves insertados una interpolación Suave.

Visualización de los claves sobre un clip de Color en la Línea de tiempo¶
La gráfica mostrada en el clip de la Línea de tiempo luce como una rampa recta. Esto es porque, al inicio, el clave en el fotograma 0 tiene una interpolación Lineal y, al final, no existe ningún otro clave posterior al segundo fotograma insertado en este ejemplo. En cualquier otro caso tanto el comienzo como el final del segmento tendría una pendiente progresivamente decreciente.
Pero, ¿qué es lo que está sucediendo aquí?
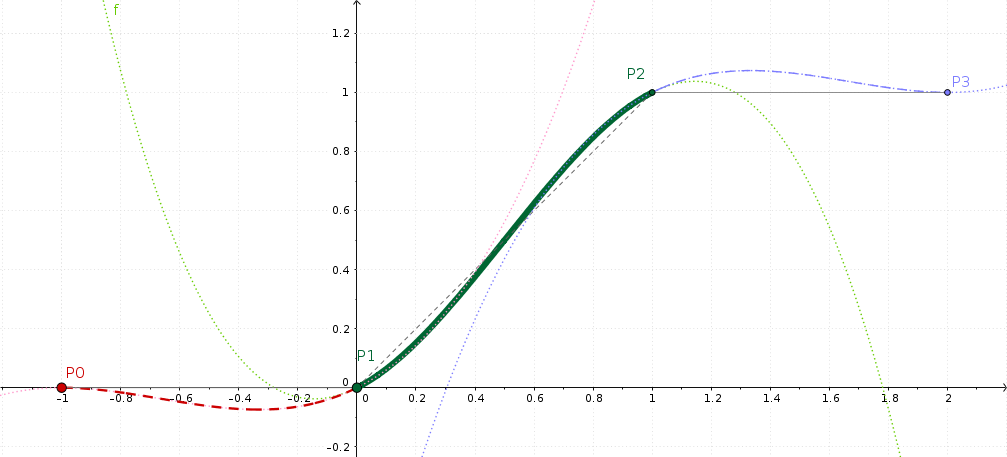
Visualización de GeoGebra de una interpolación de tipo Catmull-Rom¶
Existe esta herramienta de código abierto en línea GeoGebra que permite probar las operaciones matemáticas utilizadas por el motor MLT, usado por Kdenlive.
Esta figura muestra dos fotogramas clave P1=0 y P2=1, que conforman una rampa típica. En caso de que ya se lo estén preguntando: no es relevante en qué fotogramas exactos se encuentren los claves individuales.
La interpolación suave que MLT calculará se muestra como una línea gruesa de color verde, ligeramente flexionada en forma de letra S mayúscula.
Si se observa detenidamente, tanto la pendiente inicial como la final de la línea verde no son horizontales - o al menos no tanto como se esperaría en un principio.
Surge la pregunta ¿qué son los otros dos claves marcados como P0 y P3 y para qué sirven? Bueno, sucede que las operaciones matemáticas que suceden tras bambalinas siempre necesitarán cuatro claves para ser capaces de calcular una interpolación de un segmento entre dos claves cualesquiera. Y en caso de que no existiera un clave anterior (P0) o siguiente (P1), entonces se repetirían los valores de los claves (P1) y (P2) en cada extremo respectivo del segmento.
Sobrepaso en la cima de la rampa¶
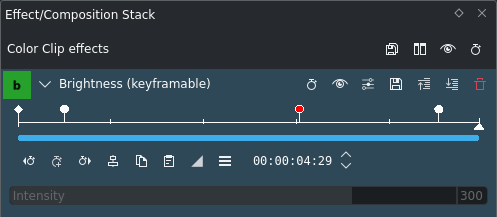
Fotogramas clave en el efecto Intensidad¶
Ahora se insertará un tercer clave, para que se forme una meseta en la parte alta de la rampa. Tal como se muestra en las capturas de pantalla.
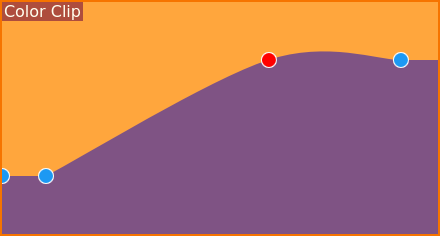
Visualización de los claves sobre un clip de Color en la Línea de tiempo¶
Ahora se puede apreciar una joroba claramente visible, en lugar de una meseta recta con el valor de los dos últimos claves. Bueno, si bien esto luce suave, no es exactamente lo que se esperaba lograr. Entonces, ¿por qué sucede esto?
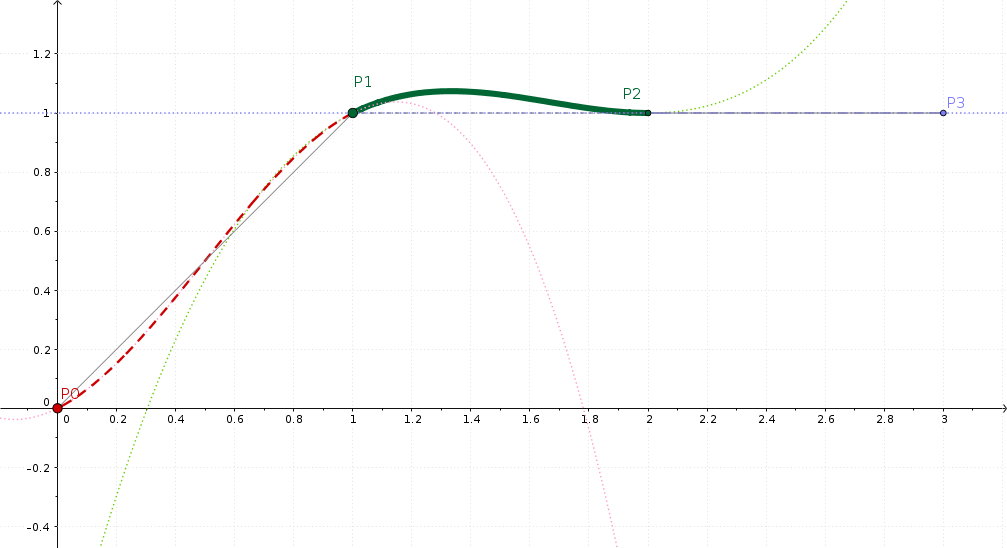
Visualización de GeoGebra de una interpolación de tipo Catmull-Rom¶
Esta es ahora nuestra rampa con una meseta: P0=0, P1=1, P2=2. No es importante la numeración de los claves.
¿Se esperaba que la meseta fuera, bueno, plana? ¡Por supuesto que sí! Pero ya se habrá podido notar que no es esa la forma en que Kdenlive se comporta. En lugar de eso, las operaciones usadas para la interpolación producen que los valores interpolados sobrepasen los valores de los propios claves, tal como se muestra en la figura.
Lo que realmente hacen la operaciones internas es esto: la interpolación es suave, por lo cual la pendiente hacia la izquierda de P1 es la misma que hacia la derecha de P1. Sí, se trata de un tipo de “suavidad” diferente a lo que se estaba esperando.
Si en vez de eso se deseara que la meseta fuera recta, deberá configurarse el modo de interpolación del clave P1 en Lineal. A propósito, esto no alterará el comportamiento del segmento anterior de la gráfica de ninguna manera. Se producirá una flexión abrupta en el clave P1, pero afortunadamente probablemente esto no será perceptible en la gran mayoría de las situaciones.
Subida y bajada de la rampa¶
Fotogramas clave en el efecto Intensidad¶

Visualización de los claves sobre un clip de Color en la Línea de tiempo¶
Se agregará ahora un cuarto clave, por lo que se tendrá: primero una rampa ascendente, luego un período plano y luego una rampa descendente. Una configuración bastante usual de fundido entrante y luego saliente.
Y qué está sucediendo: tenemos una joroba, pero no una meseta plana en la sección media.
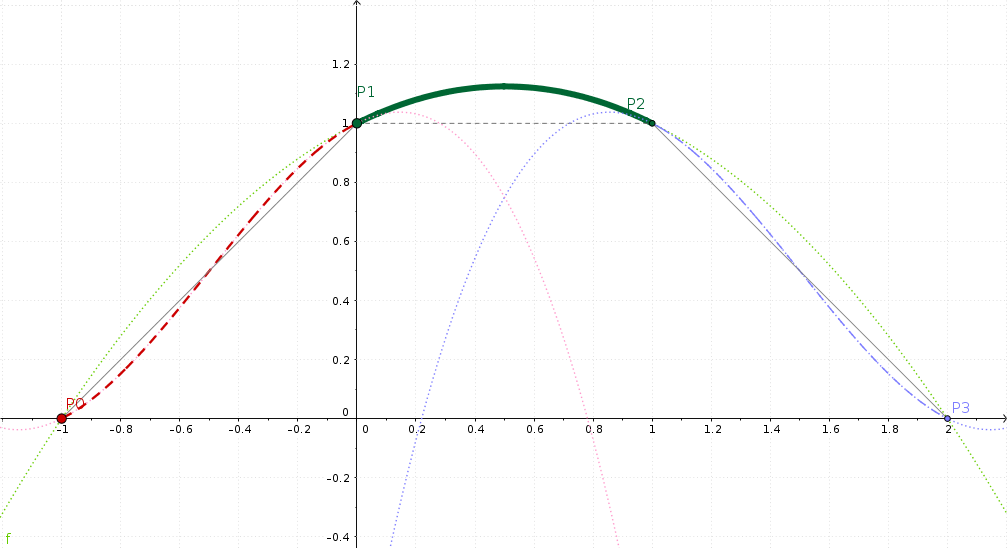
Visualización de GeoGebra de una interpolación de tipo Catmull-Rom¶
Esta vez, fijaremos la atención en la sección central, entre los claves P1 y P2. Hacia la izquierda, se ve la rampa ascendente, hacia la derecha la descendente.
Nuevamente, suave ahora significa que no se producirán flexiones abruptas en los segmentos. En vez de eso, las pendientes hacia la izquierda y la derecha serán continuas en los puntos P1 y P2; esto es, en la sección central. Y esto es lo que causará que los valores interpolados en esa zona sobrepasen el valor de los propios claves.
Hacerlo nuevamente plano¶
Claves suaves en el efecto Intensidad¶
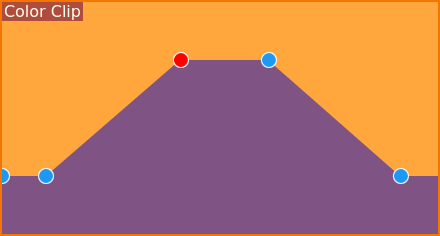
Ahora, ¿cómo es posible obtener una meseta superior plana? Afortunadamente esto será sencillo de lograr, tal como se puede apreciar en las imágenes.
Notas
- Lecturas adicionales
Como seguramente (o no tan seguramente) se recordará, el motor utilizado por Kdenlive para todas sus operaciones con medios, es MLT Multimedia Framework. Si bien MLT soporta una interpolación suave (smooth interpolation) desde alrededor de 2013, Kdenlive llegó más tarde con su soporte de los tres modos de interpolación: lineal, escalonada y suave. Tal como se puede observar en el código fuente de MLT (source code), la interpolación suave es realizada usando curvas de tipo Catmull-Rom (Catmull-Rom spline). En particular, MLT utiliza la llamada variante uniforme, dada su simplicidad. La contra de esto es que este tipo de suavizado suele tener una tendencia (no siempre deseada) al sobrepaso de las curvas, especialmente en el momento menos esperado.
- Fuentes
El texto original fue enviado por el usuario TheDiveO al (ahora desaparecido) blog kdenlive.org. Para esta documentación, ha sido tomado desde kdenlive.org, actualizado y adaptado para que coincida con el estilo de esta documentación.